- For the E-UTRAN protocol stack, it provides:
LTE release 8.6 compliant and a subset of release 10 features;
- Implements the MAC, RLC, PDCP and RRC layers;
- protocol service for all Rel8 Channels and Rel10 eMBMS (MCH, MCCH, MTCH);
- Channel-aware proportional fair scheduling;
- Fully reconfigurable protocol stack;
- Integrity check and encryption using the AES and Sonw3G algorithms;
- Support of RRC measurement with measurement gap;
- Standard S1AP and GTP-U interfaces to the Core Network;
- IPv4 and IPv6 support.
Evolved packet core network features:
- MME, SGW, PGW and HSS implementations. OAI reuses standards compliant stacks of GTPv1u and GTPv2c application protocols from the open-source software implementa- tion of EPC called nwEPC ;
- NAS integrity and encryption using the AES and Snow3G algorithms;
- UE procedures handling: attach, authentication, service access, radio bearer establishment;
- Transparent access to the IP network (no external Serving Gateway nor PDN Gateway are necessary). Configurable access point name, IP range, DNS and E-RAB QoS;
- IPv4 and IPv6 support.

DL-SCH/PDSCH Processing in the PHY Layer

Now you may have a question. Is this the end of the process ? Are these data get directly transmitted out of the antenna ? Unfortunately No. The output of this complicated process become the input (starting point) of another complicated process as shown below. I means there are a lot of stuffs you have to study pulling the hair -:)
< 36.211 - Figure 6.3-1: Overview of physical channel processing >
The baseband signal
representing a downlink physical channel is defined in terms of the following
steps:
Step-1 - scrambling of coded bits in each of the
codewords to be transmitted on a physical channel
Step-2 - modulation of scrambled bits to generate
complex-valued modulation symbols
Step-3 - mapping of the complex-valued modulation
symbols onto one or several transmission layers
Step-4 - precoding of the complex-valued modulation symbols on each layer for transmission on the
antenna ports
Step-5 - mapping of complex-valued modulation symbols
for each antenna port to resource elements
Step-6 - generation of complex-valued time-domain
OFDM signal for each antenna port

Transport Block:::::::::::::;
LTE Downlink Transmitter Model:
CRC is a kind of Error Check technology and stands for Cyclic Redundancy Checksum. The way it is used can be illustrated as follows. More detailed explanation about the concept and application of CRC is described in CRC in Error Check page. However, I decided to create a separate page for this topic mainly to deal with some examples in very detail. I want to explain on these examples in more practical way rather than too much theoretical way (If you are interested in the theoretical background, you can look into 'division of polynomial in Galois Field 2').
Example 1 >
This example itself came from an example in Ref [1]. However, the way I explain on this would be pretty much different from the ref [1] or most of textbooks. I tried to write down every steps as I am calculating the checksum by hand.
Most of the CRC problems are given as follows. You will be given a generator polynomial and a message data from which you need to calculate the checksum bits
Before you jump into solving the problem, let's rewrite the given information into a little bit different format (as in red)
Once you get these information, build a binary division equation as follows (as you see, the dividend is created by combining the given message data and trailing zeros.
If you are familiar with binary operation (GF(2) polynomial division), just drawing the equation above would be enough and you may directly write down the solution as follows.
With the checksum that was calculated above and the message data, you can create the codeword that is to be transmitted. Codeword = Dividend + Reminder =>111001010000+0100
CRC attachment to MIB – The generated CRC is attached to
the MIB payload after which the size of the payload will be 40 bits (24 bit of
MIB + 16 bit of CRC)
Convolutional encoding – A tail bit convolutional encoding is performed
over the 40 bits and the output is 3 streams of 40 bits each
Rate matching – The rate matching here is nothing but a repetition
coding, where the 3 streams of size 120 bits (40×3 bits) is just repeated 16
times to get 1920 bits. The repetition rate is very high since the MIB is a
very vital information and the UE cannot afford to lose it.
Scrambling – These 1920 bits are scrambled with a scrambling sequence as
long as 1920 bits
Modulation (QPSK) – A QPSK modulation is performed over these 1920 bits
to obtain 960 complex QPSK symbols (Symbols = Total no of bits/Bits per Symbol)
This is the basic operation for PBCH encoding, but since the PBCH has to be
transmitted every 10 milliseconds on subframe 0 of all radio frames, the PBCH
modulation buffer is divided into 4 sub-buffers each as long as 240 complex
symbols. Each sub-buffer is transmitted over PBCH and by the time the last sub
buffer is transmitted on PBCH, a new MIB is arrived from higher layer which is
again encoded using the above method and the process continues
Channel Coding Processing for DL SCH/PCH/MCH
First as a disclaimer, I am very early stage of studying this field. For a long time since I joined into the wireless communication, this kind of processing has always the part that I was so eager to undersand but eventually gave up. In LTE as well, the document like 36.211, 36.212 were mysterious specification to me. I have always wondering "How those guys can implement real device(PHY) just by reading these thin, vague, cloudy (at leas to me) documents ?".
Very recently an expert in this area helped me so much to get some insight/big picture to start with. (I still think several month to go to be able to draw detailed picture for this, but getting the initial big picture would be the most important step).
Here goes my first picture and this will get more detailed illustration later... so keep checking this part if you are interested.
The first picture you have to be familiar (don't try to memorize... just see this as often as possible and just make it familiar) . This figure is from 36.212.
Let's just make a two important bulets here. Whatever a processing unit is, the first and most important steps you have to understand is "What is the input ?" and "What is the output ?".
What is the input of this whole process ? It is a transport block.
What is the output of this whole process ? It is a series of IQ data to be transmitted from PHY.
So the whole purpose of this process is "to convert a transport block (from MAC) into a series of bit stream data to be transmitted".
< 36.212 - Figure 5.3.2-1: Transport block processing for DL-SCH, PCH and MCH.>
Now let's look into each step of the process.
The first step is pretty simple. Just adding 24 bits of CRC block to the end of the input (transport block).
The second step is as follows. It is splitting the big transport block into multiple small blocks and add another CRC to each of the split chunks. Sounds simple ? but there is a couple of things to make it tricky. Why do we need to split the block ? Do we always to have to split the input block ? It would be understandable to split a very large input block into multiple smaller block, but if we have to split even a small input block, isn't it inefficient ?
The generic answer is that the process split the input block only when the block is very large.
Then the question is "How large it would be to be splitted ?" In LTE case, 6144 (bits) is the number. (See 5.1.2 Code block segmentation and code block CRC attachment of 36.212)
Next step is the famous Turbo Coding step. I am not able to explain on how turbo coding works in easy/plain language mainly because I don't understand it clearly. But for now, let's just focus on only one fact. If you see the turbo coding block diagram in 36.212. You would see that one bit input become 3 bit output as it goes through the turbo coding processor (It means the coding rate is 1/3). In this process, one input row generate three rows of output as follows.
Next step is Rate Matching step. This is the most mesterious part to me. The generic Idea is like this. I said Turbo coding generate three rows of output for each row of input. In this rate matching process, the each set of three rows of input stream became one row of bit stream. The question is "How to convert the a set of three row into one row ?" Is it just by concatenating the three row into one long row ? Is it just random mix of the three row ? Is it by interleaving the three row into one ?".
This is the question you have to find the answer from 5.1.4.2 Rate matching for convolutionally coded transport channels and control information of 36.212. Good luck with your endeaver -:) I think it will take a couple of month for me to understand this even with a good tutor around me.
Just adding another big picture to this rate matching step, take a quick look at the following figure from 36.212. You see the three lines of Turbo coding output gets into this rate matching block and comes out as a single line of bit stream. Our goal is to understanding the detailed process of "interleaving", "BitCollection", "Bit Selection and pruning" procedure.
< 36.212 - Figure 5.1.4-1. Rate matching for turbo coded transport channels >
Next is the last step which is relatively simple. Combine the multiple rows of imput into one long bit stream as shown below.
==============Channel Coding=====
In this page, I will go through Matlab/Octave functions for communication system within a context of a whole process but in step-by-step manner. You would have seen many other resources elsewhere explaining on these functions, but most of the material that I have seen was purely for showing the syntax of each functions. So it was very hard for me to understand practical meaning of those functions within a whole communication process.
- Coding(Encode/Decode)
- Why Coding ?
- Downside of Coding
- Fundamental Questions of Coding
- Block Code
- Overview
- Meaning of 'Linear'
- Meaning of 'Cyclic'
- Generation of Linear Block Code
- By Generation Matrix
- By Generator Polynomial
- Galois Field
- gfconv
- Examples of Channel Coding
- Hamming
- Cyclic
- Linear
- Convolutional Code
- Representation of Convolutional Code
(With Reference to Lec 2 | MIT 6.450 Principles of Digital Communications I, Fall 2006 (YouTube) )
Looks very simple. Then why the text book about this is so thick ?
It is because "We want to implement Efficient process". What do you mean by "Effiecient process" ? It may roughly mean "a process to send data using as less number of bits as possible" and "a process to be guaranteed to work". All that the thick text book is trying to say is "How we can make the efficient process ?", "How do you represent it in mathemaical form ?", "How do you prove (in mathemtical way) that it is efficient and always work?"
In real work, most of engineers doesn't care about this. There are only handsful of persons who digest all those textbook issues and come out with 'what they think is efficient process' and produce 'technical specification (e.g, 3GPP)'. Around 99% of us just follows the specification. That's why we don't read the text book after we graduate from university and still can survive -:)
There would be a couple of variations of the definitions of Source Coding depending on the context. The first type of definition is 'to convert the original data(user data) into a certain binary sequence' which is illustrated as below.
(With Reference to Lec 2 | MIT 6.450 Principles of Digital Communications I, Fall 2006 (YouTube) )
Another type of definition for source coding (according to Ref [2]) is to convert a source data into a form that can minimize the bandwidth that are required to transmit the data. Simply put, it is just another name for 'Data Compression'.
Again, It doesn't look that complicated. Then why the text book about this is so thick ?
Same answer as above.
Channel Coding is a method to replace 'original data bits' with 'some other bits (normally longer than the original bits)'. For example, the simplest coding would be as follows :
0 --> 0000 : replace all '1' in orginal data into '0000'
1 --> 1111 : replace all '1' in orginal data into '1111'
Another example of coding would be addition of parity bits as in RS 232 communication
original seven bit data --> original seven bit data + one parity bit
In communication system, we usually call 'the original data' as a 'message' and call the ecoded data as 'Codeword'. In all encoding process, the length of Codeword is greater than the length of 'message', in means that in coding process some additional bits are added to the original data(message) and this additional bits are called 'redundency bits'.
Why Coding ?
Why do we need this kind of Coding ?
Most of the experts in this area would come out with something like 'Shannon's theorem'.. but let's just look at this in intuitive way rather than bringing up such a scary words.
Let's look at the simple wireless communication process that we went through in previous section. In this process, what do you think is the biggest problem ?
Just give your self a moment to think before you go on.
The answer is the 'noise' which is added by 'Channel'. As you can guess, this noise would make a lot of errors while the reciever is demodulate the received signal into the bit stream.
What would be the solution for this problem ?
We can think about two possible options.
- Make the channel noise-free. (Construct the channel in such a way there is no noise)
- Use some method to detect and correct the error
Which option do you prefer ? You would know that the first option would be almost impossible especially in wireless communication. If it is wired communication, at least you can make some try to reduce the noise in the channel but in wireless it is almost impossible to remove the noise directly from the channel.
It means the only option is to develop some method (algorithm) to detect and correct the error caused by the noisy channel. This is the main motivation for 'Coding'.
Main idea of Coding is to add some additional bits (we call this as redundancy bits) to original data in a very special way (not in a random/arbitrary way) so that they can be used to detect the exact location of error and correct it.
In communication chain, following two blocks are added for this purpose. 'Encoding' is the process of adding redundancy bits and 'Decoding' is the process of extracting the error corrected bits from the received data.
Usually Encoding/Decoding blocks locate as shown below. Encoding takes in the bits stream and produce coded bit stream.
Getting in further detail, this encoding often happens in two steps called Source Coding and Channel Coding, but in this post I will just describe this process as a single step.
Downside of Coding
In previous section, I said "Encoding/Decoding is mainly for detecting/correcting erros generated in communication process". It is very good and important step. But once you gain something, you would lose some other things. It is almost nature of everything including our life.
What is the gain for Encoding/Decoding ? It is the received data with less or almost no error.
What is the loss ? What is downside of this process ? Following are the major issues caused by Encoding/Decoding process.
- Data Transmission Overhead (Due to redundancy bits)
- Complicate the data transmission and reception process (due to encoding/decoding algorithm)
Fundamental Questions of Channel Coding
As I said earlier, Coding is adding some redundancy bits to original data and these redundancy bits will be used to detect and correct error in decoding process. There are many different Encoding/Decoding algorithms which has it's own advantage and disadvantages. So we would always have the following question when we implement Coding/Decoding Blocks.
- How many bits of redundancy bits I have to add to minimize the number of redundancy bits and maximize the error correction ?
- Which Encoding/Decoding algorithms would be the best for the communication system I am implementing. .
There would not be a simple/clear-cut answers to these questions.
In general, the more redundancy bits you add, you would have higher error detection/correction capability. But the more redudancy bit you add, the less throughput you would get because larger portions of transmitted bits should be allocated for the redundancy bits, not for the information that you want to send. So you have to carefully determine how many bits you would allocate for the redundancy bits.
Fortunately in most mobile communication system, somebody else has already determined the answer to these questions. For example, in LTE or WCDMA system.. 3GPP specification specifies all the details of Encoding/Decoding process and you don't have to worry about these questions.
For example, in LTE case, 3GPP 36.212 specifies the Coding algorithm and related parameters as shown below. Chapter 5 of the specification provides all the detailed parameters to implement the coding process.
From now, I will introduce some of the basic functions in Matlab/Octave related to Encoding/Decoding. My goal is to extend this section to Turbo Coding/Convolution Coding which is most widely used in mobile communication system, but I am not sure by when I can achieve this goal. Let's just start with the simple things first.
Overview
Block Code is an encoding method in which we split the whole input data stream into small blocks and replace the small block (Message) with another small block(Codeword).
This process can be illustrated as shown below. The small block getting into the Encoding function is called a 'message' and the block getting out of the Encoding function is called 'Codeword'. We also express this process in a symbol (n,k). n is the number of bits for codeword(output) and k is the number of bits for message (input). n is always greater than k, meaning the length of output (Codeword) is always longer than the length of input(Message).
One example of block code is as shown below. In this example, we split the input data stream into 4 bit chunks and replace each of the chunks with 7 bit chunk. The mapping table between each possible 4 bit chunk(input = message) and 7 bit chunk(output = codeword) is shown below.
Meaning of 'Linear'
'Linear' when you say 'Linear Coding' means a set of code in which any linear combination (modular 2 sum) of two codes within the set results in a code which also belong to the original set. Let's assume that you have a set of codes as follows. Take out any two codes from the set and take modular 2 sum of them. The result is also a member of the set as shown below. Take any other two codes and try yourself.
Meaning of Cyclic
'Cyclic' is a set of code in which a code can be generated by cyclic shift of another code in the set. or in other word, any number of cyclic shift of a code in the set also fall within the set. For example, let's assume that we have a code set which is made up of following four codes. If you look into each of these codes, you would notice that any of these codes can be created by the cyclic shift of another code as illustrated below.
Take the code (0 1 0 1 0 1) and cyclic shift right by one and it gives (1 0 1 0 1 0) which is also a member of the set.
Take the code (0 1 0 1 0 1) and cyclic shift right by two and it gives (0 1 0 1 0 1) which is also a member of the set.
In short, in this set .. whatever code you take and however many times you do cyclic shift, the result is always within the original set.
Generation of Linear Block Code
Now you may ask "how can I create a mapping table as shown above ?".
The simple answer would be "You can create it in any way as you like ?".
Really, Is it true ? Can I use any arbitrary mapping table as pops up in my mind now ?
Yes, you can. but it doesn't mean that what you created in arbitrary way would be 'efficient' mapping (coding).
Then what would be the efficient coding ? There may be multiple answers to this, but some common answer would be
- Capability of detecting/correcting with minimum number of redundancy bits.
- Easy of implementatione
Generation By Generation Matrix
One of the way to perform coding is to use what is called 'Generator Function'. You might come across this term in any kind of materials related to 'Coding'. My first response when I first heard of this function was 'What the hell, is it ?'. Is it something like those functions that we learned in high school ? It looks similar to what we learned in high school days.. e.g, g(x) = x^4 + x^2 + 1, but the way they are used looks pretty different from high school.
My next question was "Why they call it 'Generator Function' ?".
I would not try to give you answer to these question here.. you will get it as you proceed. What I am trying to say is "Don't feel yourself as stupid if you have the same questions" -:).
Generator Function is a kind of 'Binary Function' which can perform 'coding' (Convering a message to a codeword) in following manner.
Expressing the equation in more detailed form, it can be expressed as shown below.
The best way to understand the real meaning of the equation above would be by example. Here goes one example.
Let's suppose you have four generating functions
g1(x) = 1 + 1 x + 0 x^2 + 1 x^3 + 0 x^4 + 0 x^6 + 0 x^7 = 1 + x + x^3
g2(x) = 0 + 1 x + 1 x^2 + 0 x^3 + 1 x^4 + 0 x^6 + 0 x^7 = 0 + x + x^2 + x^4
g3(x) = 1 + 1 x + 1 x^2 + 0 x^3 + 0 x^4 + 1 x^6 + 0 x^7 = 1 + x + x^2 + x^6
g4(x) = 1 + 0 x + 1 x^2 + 0 x^3 + 0 x^4 + 0 x^6 + 1 x^7 = 1 + x + x^2 + x^7
you can pack these equations into a matrix as shown below. (Note that the lowest order comes leftmost).
Let's suppose you have a message as shown below.
m = (1 1 0 1)
Now, let's figure out codeword for this message (figure out the output bit stream when this message go through the encoder block). This is the point where we use the generator function shown above. The process to calculate the codeword using the generator function is as shown below.
For practice, try all the messages shown in overview section and check if your calculation matches the codewords in the section.
Now let's take a high level view of generator function (generator matrix) and see if there is any recognizable pattern. It is as shown below.
You may notice followings right away.
i) The number of rows is same as the length of message (number of bits in message)
ii) The matrix contains the k x k Identity matrix, where k is the length of the message
Now you would ask another again. How can I get these generator functions ? (How can I know which generator functions I have to use ?). Don't worry.. in most case these functions/matrix will be given to you from the specification of the communication system. (Of course, there is theoretical background that justifies those generator functions given by the specification and you can refer to Communication Text Books or surf on internet for it. I would not get further into it). In think, just understanding the meaning of the generator functions and how to use them to implement 'encoder' block would be enough in most case.
Now let's look into the codebook we generated from higher level. As shown below, you would notice that the codebook contains the message part as it is at the end and redundant bits at the beginning. This is one of the characteristics of what we call 'linear block coding'.
Generation by Generator Polynomial
Now you may have a question. Is this the end of the process ? Are these data get directly transmitted out of the antenna ? Unfortunately No. The output of this complicated process become the input (starting point) of another complicated process as shown below. I means there are a lot of stuffs you have to study pulling the hair -:)
< 36.211 - Figure 6.3-1: Overview of physical channel processing >
=======PDSCH Physical Channel Processing=========
Physical Channel Processing
This is the process that convert the bit stream coming out of channel encoding process into radio frame data to be transmitted by each antenna.
Overall flow is as shown below and I put the 3GPP specification for each steps. This process is also the one that would be very difficult to understand in very details unless you follow each steps of the procedure written in the specification. But this process is described in a very short mathematical format and it is hard to describe in other way without losing the clarification.
In this section, I would like you to grasp the basic idea of each step.
At lower part of the diagram, I labeled the data format of each step. If you follow those labels, you would know at which steps bit stream is being handled and at which steps I/Q data is handled etc.
One good way for you to study this procedure would be to classify the procedure into several specific cases like SISO, Diversity, 2x2 MIMO etc and mark the path for each case as shown below.
Video Tutorial : http://www.youtube.com/watch?v=u5lStqUlMgU&feature=related
< SISO >
As shown below, marked in red/blue arrow, only one codeword (transport block) comes into the process and directly goes to the antenna. In this case, layer mapper and Precoding steps do almost nothing.
< Tx Diversity >
As shown below, marked in red/blue arrow, only one codeword (one transport blocks) comes into the process and split into two stream (layers) by the layer mapper and finally go out through the two antenna.
< 2 x 2 MIMO >
As shown below, marked in red/blue arrow, two codewords (two transport blocks) comes into the process and goes through the layer mapping without any modification and finally go out through the two antenna. In this case, data goes through very complicated precoding process. As described in the specification, there are three sub steps of procoding process as specified in 36.211 6.3.4.2.1, 36.211 6.3.4.2.2, 36.211 6.3.4.2.3. Depending on whether the 2 x 2 MIMO is Closed Loop Mode or Open Loop Mode, the different combination of the substeps are applied.
Precoding
Unfortunately I don't know how to explain this part in plain language without using any mathematical tools.
As you see in the following diagram, Precoding is the process that is between Layer Mapper and Resource mapper. In practice, this precoding is the process that rearrange the IQ constellation into the form that can maximize the throughput to the multiple reciever antenna.
To make the process and understanding simpler, let's assume that we are only focusing on two antenna case. If it is two antenna case, the block diagram around the Precoding looks as follows. (TM4 is using this configuration)
The only way to understand this concept to the skin would be to try this yourself and play with all these parameters like your toys. To help this, I created a small octave code and attached here. (I create this code in Octave which is a Matlab like GNU program, but I guess it will run in Matlab without any modification. I tried to write the code so that I can run on both program but I haven't tested it in Matlab myself).
Note : If I expand the transformation shown above into a 2 x 2 case to give you more concrete idea, it can be illustration as follows. Since all of the data used here are complex numbers (Real = I, Imaginary = Q), the result of operation may not be so intuitive to you. If you are really interested in understanding the result of transformation, try this transformation with your own program or pen-paper calculation on your own. At least, play with the matlab code that I created and linked here.
Following is the real Downlink signal coming out of a LTE network emulator. I capture the signal and analyzed it with a vector spectrum analyzer with LTE analysis functionality.
Now let try apply the CDD. I would recommend you to try investigate on what's is CDD in practical sense and what would be the advantage of applying CDD. Here I would only show you the result of the CDD application. The Octave code is here. (I create this code in Octave which is a Matlab like GNU program, but I guess it will run in Matlab without any modification. I tried to write the code so that I can run on both program but I haven't tested it in Matlab myself).
Following is the case where a single layer data stream gets transmitted by two antenna. Overall procedure is as follows. (TM6 is using this configuration)
If we apply the Layer 1 code book to a sequence of data, we will get the constellation as follows. If you briefly see the constellation, you don't find any differences in terms of constellation except overall amplitude gets smaller after going through the precoding block. But if you following through the precoding process for each one (single) constellation, you will understand the differences.
The Octave code is here. (I create this code in Octave which is a Matlab like GNU program, but I guess it will run in Matlab without any modification. I tried to write the code so that I can run on both program but I haven't tested it in Matlab myself).
Note : If I expand the transformation shown above into two antenna case (diversity) to give you more concrete idea, it can be illustration as follows. Since all of the data used here are complex numbers (Real = I, Imaginary = Q), the result of operation may not be so intuitive to you. If you are really interested in understanding the result of transformation, try this transformation with your own program or pen-paper calculation on your own. At least, play with the matlab code that I created and linked here.
As I mentioned above, if you just see the overall constellation, you don't find any differences in terms of constellation except overall amplitude gets smaller after going through the precoding block. But if you following through the precoding process for each one (single) constellation, you will understand the differences. Following sequences of plots shows you 'Precoding' result of each points with each precoding (transformation) vector. Colored spots represents the constellation (I/Q data) coming(I/Q data) out of Layer Mapping block and coming into Precoding block. Black spots represents the constellation coming out of the Precoding block. You would notice that each of the colored spots creates two black spots. Even for the plot with only one black spots, it is the superimposed result of two black spots. Each of the black spots gets transmitted by each of the antenna.
The Octave code is here. (I create this code in Octave which is a Matlab like GNU program, but I guess it will run in Matlab without any modification. I tried to write the code so that I can run on both program but I haven't tested it in Matlab myself).
MIMO (Multiple Input Multiple Output)
I think everybody would know what MIMO is. Simply put, it is a technique to increase the data throughput by using multiple transmitter antenna and multiple reciever antenna. So.. overall concept is simple, but detailed process and implementation is not as simple as you may think. Unfortunately -:), it would be almost impossible to understand the details without going through underlying mathmatics. Actually math itself is not that complicated but interpreting the math and translate the math into real implementation is difficult. I hope my math section in this site would helpful on this. (Please see the Engineering Math - Matrix as you go along this section).
Try googling "MIMO introduction", "MIMO Tutorial" for general understanding . I will try to cover the math part here. I will use 2 x 2 MIMO in this section for simplicity.
In case of 2 x 2, overall data transmission process can be illustrated as follows. The red arrow and four blocks (h11,h12,h21,h22) between the two antenna is to illustrate the possible data path between the two Tx and two Rx antenna.
h11, h12,h21,h22 are special numbers (coefficient) to show how much of the data is going through each of the possible path. The greater the value is, the larger portions of data is being transmitted in that path. A matrix which is made up of these channel path coefficient is called "Channel Information Matrix". The reciever and transmitter relationship is represented as follows.
As I said the math itself is very simple. It would be like a first example at the first chapter of any linear algebra book. The important this is how to interpret this equation into real implementation. If I interpret it in an illustration, it would be as the path represented in green arrows. By this way, we can mathematically represent the recieved data (data distorted by the air path between transmitter and reciever antenna), but just calculating the recieved is not our goal (not the function of the reciever). Our goal is to extract/figure out the 'transmitted data (original data)'. Mathematically this is also simple and it is represented in green arrows.
As you see in the process illustrated in green arrow, to recover the transmitted data (original data) from the received data we need to take inverse of the channel information matrix. Unfortunately there are a couple of issues with this method.
i) Not all matrix is invertable. There are some matrix for which inverse matrix does not exists. (Please refer to Matrix section and see what kind of matrix is the one which is not invertable).
ii) Calculating the inverse matrix is not the simple process.
To workaround these problems, we change the channel information matrix into three matrices by the method called SVD(Singular Value Decomposition). See the SVD section in Marix page and clearly understand the meaning of this process. Probably my page would not be enough to give you full understanding about SVD. Google as much materials about this as possible and try to have some "Intuitive" understanding of the concept.
When we apply any mathematical technique in engineering area, it should be meaningful in the engineering sense and should be implementable. The meaning and implementation of SVD can be illustrated as follows.
The important point is that by implementing this method, we can express the channel information matrix as a simple 'diagonal matrix'. That diagonal matrix is expressed as follows and can be illustrated as follows. Isn't it look simple and clear ? -:)
For some MIMO implementation (e.g, TM4 in LTE = Closed Loop MIMO), you estimate the channel and select a specific precoding matrix and send it back to the receiver as shown below.
The algorithm by which UE select the codebook which is best fit for the channel at specific moment is as follows.
Once a specific codebook element (precoding matrix) is selected as shown here, that precoding matrix is used to transform the incoming bits as explained in Precoding section.
Integrity Protection Procedure
My perception of any process is "a black box that convert a set of inputs into a set of output". So for any process, I usually tries to define what is the inputs and out is the final outputs.. and then try to find the all of the steps one by one to convert the input into the outputs.
If I define LTE Integrity Protection Procedure with this logic, it would be "a process that convert 'K' value from USIM into PDCP MAC-I and NAS MAC(Message Authentication Code)". Describing this process with illustration would be as follows. Just try to go through this illustration whenever you have chance and try to have your own idea first.
The process described here apply only to C-Plane data. (Refer to 33.401 for the detailed description of each of the steps).
====================OFDMA Generation=================
·
An OFDMA signal is based upon a set of orthogonal subcarriers.
Resources are shared by allocating a subset of the subcarriers to each user
·
The subcarriers are orthogonal because when sampling one
subcarrier at its peak, all other subcarriers have zero amplitude
·
The subcarriers are tightly packed to help make efficient use of
the spectrum
·
Information is transferred by modulating each
subcarrier. For example, the modulation applied to each subcarrier could be
QPSK,
·
16QAM or 64QAM
·
The Inverse Fast Fourier Transform (IFFT) is
used to generate a time domain OFDMA symbol from a combination of the modulated
subcarriers
·
A significant benefit of OFDMA is its tolerance
to propagation channel delay spread
·
OFDMA is tolerant to delay spread because its
time domain symbols have relatively long durations. This is possible because
data is transferred in parallel (across subcarriers) rather than in serial
Ø
a typical OFDMA symbol for L TE has a duration
of 71.35 uS (defined as 1 I subcarrier spacing of 15 kHz+ an overhead for the
Cyclic Prefix)
Ø
a 10 MHz OFDMA channel could have 600
subcarriers spaced at 15 kHz generating a modulation symbol rate of 600 I 71
.35 uS = 8.4 Msps
Ø
if transmitting data in serial, 8.4 Msps would
require a symbol period of 1 I/8.4 x 10 6 = 0.12 us.
OFDMA SIGNAL GENERATION
Ø The set of modulated Physical Channels and Physical Signals are mapped onto the grid of resource elements
As shown in Figure 11, the transmitter processes one column of resource elements at a time
Ø
The first resource element from the top half
(counting upwards) is multiplied by a complex phasor rotating at +15 kHz (1 ×
subcarrier spacing). The second resource element of the top half is multiplied
by a complex phasor rotating at +30 kHz (2 × subcarrier spacing). Figure 13
illustrates the concept of multiplying a resource element by a complex phasor.
Ø
The first resource element of the bottom half
(counting downwards) is multiplied by a complex phasor rotating at -15 kHz (-1
× subcarrier spacing). The second resource element of the bottom half is
multiplied by a complex phasor rotating at -30 kHz (-2 × subcarrier spacing)
Overview
OFDM stands for Orthogonal Frequency Divisition Multiplexing. If you understand the meaning of following keywords, you would have pretty good big picfure of OFDM.
- Orthogonal
- Frequency Division
- Multiplexing
You will figure out what all these terms are about as you go through this page.
OFDM is a technology that we split a wide frequency band into many small frequencies (we call this split frequencies as subcarriers) and carry data onto each of these sub carriers as illustrated below. In other words, we 'devide a wide frequency band' into multiple small/narrow frequencies. This is the meaning of 'Frequency Division'. Since all the data on each of these subcarriers are transmitted simultaneously, we can say this is a kind of 'Multiplexing'.
Now you may have a question at this point. How small we can make it for each subcarrier (subcarrier, divided frequency) ? For example, if you are given 1 Mhz bandwidth as a fullband, how many subcarriers we are supposed to split into ? If you split it into 1000 sub carriers with 1 Khz interval and carry one bit on each sub carrier, you can transmit 1000 bits simultaneously. If you split it into 100 sub carriers with 10 Khz interval and carry one bit on each sub carrier, you can transmit 100 bits at a time.
Which option you would take ? Definately you would want to split it into 1000 sub carriers.. you would even say I want to split it into even more sub carriers.
But unfortunately it would not be possible to split it with too small intervals between sub carriers. If you split it into too many sub carriers with too small space between sub carriers, there would be much high possibility of interference between adjacent sub carriers. However, if you separate each subcarrier too much and have small number of sub carriers, you would have much less interference between sub carriers but in that case the data rate would be decreased.
As a kind of optimal solution, OFDM split the band into multiple sub carriers in such a way as shown below. In the following illustration, at each sampling point in frequency domain there is only one carrier which has non-zero value and all other sub carriers has zero value at the sampling point. It means that even though multiple sub carriers coexists they are all independent and does not influence others, this characteristics are called as 'Orthogonal'. ( If any two functions or vectors are orthogonal, it means that they are linear independent to each other. You can find the mathematical definition of Orthogonality from WiKi, but it would not be easy to figure out practical meaning of Orthogonality from it. Just simpliy think "Orthogonal" means "Independence" and "Independence" means "No interaction/interference", therefore "Orthogonal" means "No Interference")
OFDM is very good method of utilizing the given frequency wisely, but there is a drawback to this method. For this method to work efficiently the space between sub carriers should be maintained exactly at the specified position which satisfy the condition of orthogonality.
What if the space between sub carriers are not maintained accurately and they are drifting around. One example for this case is shown below. You would not see much differences when each sub carriers are plotted separately (upper plot), but you would notice the differences when all of these sub carriers are summed together as shown on lower plot.
Unfortunately, in reality there is no such an environment in which there is no frequency drift. so when you design an OFDM, first you have to determine the frequency space in which the system can tolerate the signal distortion due to frequency drift of sub carriers. (Most common sources to cause frequency drift of sub carriers would be 'Fading' and 'Doppler effect').
To give you some toy to play with the concept of OFDM and the effect of frequency drift, I put the Matlab/Octave source code that I used to create plots shown above. Try with different values for NoOfCarriers and fnoiseMax and see how the result get different.
NoOfCarriers = 11; % Put an Odd Number
f = -5*pi:pi/50:5*pi;
fnoiseMax = 0.3;
iMin = -(NoOfCarriers-1)/2;
iMax = (NoOfCarriers-1)/2;
csum = zeros(1,length(f));
close all;
fList = [];
cList = [];
subplot(2,1,1);
hold on;
for i=iMin:1:iMax,
fnoise = fnoiseMax*(rand()-0.5);
fshift = (i .* (1/pi) .* pi) .+ fnoise;
c = sinc(f .- fshift);
csum = csum + c;
fList = [fList,fshift];
cList = [cList,max(c)];
plot(f,c);axis([min(f),max(f),-0.5,1.5]);
stem((i * (1/pi) * pi) + fnoise,1,'r-');
end;
grid();
hold off;
subplot(2,1,2);
hold on;
plot(f,csum);grid();axis([min(f),max(f),-0.5,1.5]);
stem(fList,cList,'r-');
hold off;
Cyclic Prefix
Now let's look at the signal in time domain. Following is an illustraion showing two OFDM symbols in sequence.
In ideal case, there is no problem with this signal, but what would happen if the first symbol get delayed a little bit. In this case, the ending part of the first symbol will spill over into the following symbol time and interfere the next symbol as shown below. This kind of interference between different symbols are called 'Inter Symbol Interference (ISI)'.
What would be the solution to handle this problem ? You may want to prevent the signal from getting delayed. But it is not possible because we have no control over the radio channel itself(physical medium itself). So the only way is to design our system to handle this kind of situation. One simple solution is to put some time gap between symbols so that one symbol would not spill into next symbol even when it get delayed.
With this gap, the system would tolerate delay and intersymbol interference issue to a certain degree, but there is a practical issue. The issue is 'what to put in this gap ?'. Would it be good to put nothing (like turning off transmission) ? If you completely turn off the signal during the gap, it would cause issues for amplifier. To reduce this issue, we copy a part of signal from the end and paste it into this gap. This copied portion prepended at the beginning is called 'Cyclic Prefix'.
As I explained, main purpose of cyclic prefix is to reduce ISI(Inter Symbol Interference), but we can enjoy an extra advatage from generating the cyclic prefix by copying the ending part of the original symbol. It helps find the symbol boundary (the start and end of a symbol). It goes like this. Take a sequence of samples (window) with the length of cyclic prefix. Take out another sequence with the same length which is (symbol length - CP length) apart from the first sequence. And then calculate the correlation of the two sequence. If the two sequence is exactly aligned with the start and end of the symbol, the correlation would be very high because the contents within the two sequence would be almost the same.
If the two sequence (two window) does not align with the symbol boundary (start and end of a symbol), the correlation would not be high as shown below.
If you slide these two windows up and down and find the location which give you the highest correlaction, that is the slot boundary.
Example
I hope you have got the general idea on how OFDM works from previous section, but it is only a conceptual description and there would be some gap to fill in terms of details between the concept and real implementation. Let me give you an example that would give you more concrete idea than the previous concept. Overall idea for this example is based on IEEE 802.11 (WLAN specification) but this example is also missing pretty much details. However, it would give you more concrete idea about OFDM implementation.
Let's assume that you are given an OFDM specification as follows. (In most case, specification would not be given in the form of illustration like this, but it would be helpful (I am recommending) to describe the specification in graphical form.
In OFDM implemetation, the frequence at exact center does not carry any subcarrier and there are a certain number of sub carriers at both ends of the spectrum which does not have any sub carriers. This regions are called as Guard band and this is mainly to reduce the interference with neighbouring band.
Now let's follow the steps to implement an OFDM signal from the bit data we want to send. For simplicity, the modulation we are using is BPSK which carries one bit per each constellation point. According to the given specification, out of 64 sub carriers allocated for the band only 52 sub carriers are the sub carriers which can carry data bits as shown below.
For this step, first we have to generate a bit sequence which will be carried by one OFDM symbol. You can generate a random bit sequence as following way. (In real communication, nobody would use random data to transmit. If it is real communication, this data would be a document file, music or movie etc but in case of simulation, we normaly use random data).
Next step is to map the user data to each of sub carriers which is assigned for data carry. This can be implemented as follows. (At first look, this would not be clear to you unless you are very familiar to Matlab/Octave array manipulation. You may use for loops to do this, but following way would be much simpler).
With procedure described above, we have bit stream allocated to sub carrier in frequency domain. But all the communication (data transmission and reception) is happening in time domain. So we have to convert the frequency domain data into a time domain sequence as shown below. You would already know that IFFT (Inverse Fast Fourier Transform) is the tool to convert a frequency domain data into a time domain data.
Next step is to add Cyclic Prefix to the time domain data we got in previous step. Cyclic prefix generation is very straightforward, it is direct copy of some portion of data from the end and putting the copy at the beginning of the data sequence. (What is Cyclic Prefix ? Why we need this ? I will explain on Cyclic Prefix sometime later in a separate section).
Following is the Matlab/Octave code to implement all the steps described above.
TotalNumberOfSubCarrier = 64;
% for each symbol bits a1 to a52 are assigned to subcarrier
% index [-26 to -1 1 to 26]
subcarrierIndex_Data = [-26:-1 1:26];
BitsPerSymbol = 52;
close all;
figure;
% BPSK modulation
ModSequence = 2*randi([0 1],1,BitsPerSymbol)-1;
subplot(6,1,1); stem(abs(ModSequence));xlim([1 length(ModSequence)]);
TimeDomainSequence = []; % empty vector
ModSequenceForSubCarriers = zeros(1,TotalNumberOfSubCarrier);
% assigning bits a1 to a52 to subcarriers [-26 to -1, 1 to 26]
ModSequenceForSubCarriers(subcarrierIndex_Data+TotalNumberOfSubCarrier/2+1) = ModSequence(1,:);
subplot(6,1,2); stem(abs(ModSequenceForSubCarriers));xlim([1 length(ModSequenceForSubCarriers)]);
% shift subcarriers at indices [-26 to -1] to fft input indices [38 to 63]
ModSequenceForSubCarriers = fftshift(ModSequenceForSubCarriers);
subplot(6,1,3); stem(abs(ModSequenceForSubCarriers));xlim([1 length(ModSequenceForSubCarriers)]);
ModSequenceInTimeDomain = ifft(ModSequenceForSubCarriers,TotalNumberOfSubCarrier);
subplot(6,1,4); stem(abs(ModSequenceInTimeDomain));xlim([1 length(ModSequenceInTimeDomain)]);
% adding cyclic prefix of 16 samples
ModSequenceInTimeDomain_with_CP = [ModSequenceInTimeDomain(49:64) ModSequenceInTimeDomain];
subplot(6,1,5); stem(abs(ModSequenceInTimeDomain_with_CP));
xlim([1 length(ModSequenceInTimeDomain_with_CP)]);
TimeDomainSequence = [TimeDomainSequence ModSequenceInTimeDomain_with_CP];
subplot(6,1,6); stem(abs(TimeDomainSequence));xlim([1 length(TimeDomainSequence)]);
figure;
SamplingRate = 20;
[PowerSpectrum,W] = pwelch(TimeDomainSequence,[],[],4096,20);
subplot(1,3,1);plot([-2048:2047]*SamplingRate/4096,10*log10(fftshift(PowerSpectrum)));
xlabel('frequency, MHz')
ylabel('power spectral density')
subplot(1,3,2);plot(10*log10(fftshift(abs(fft(ModSequenceInTimeDomain)))));
xlim([1 length(ModSequenceInTimeDomain)]);
subplot(1,3,3);plot(10*log10(fftshift(abs(fft(TimeDomainSequence)))));
xlim([1 length(TimeDomainSequence)]);
============================================================
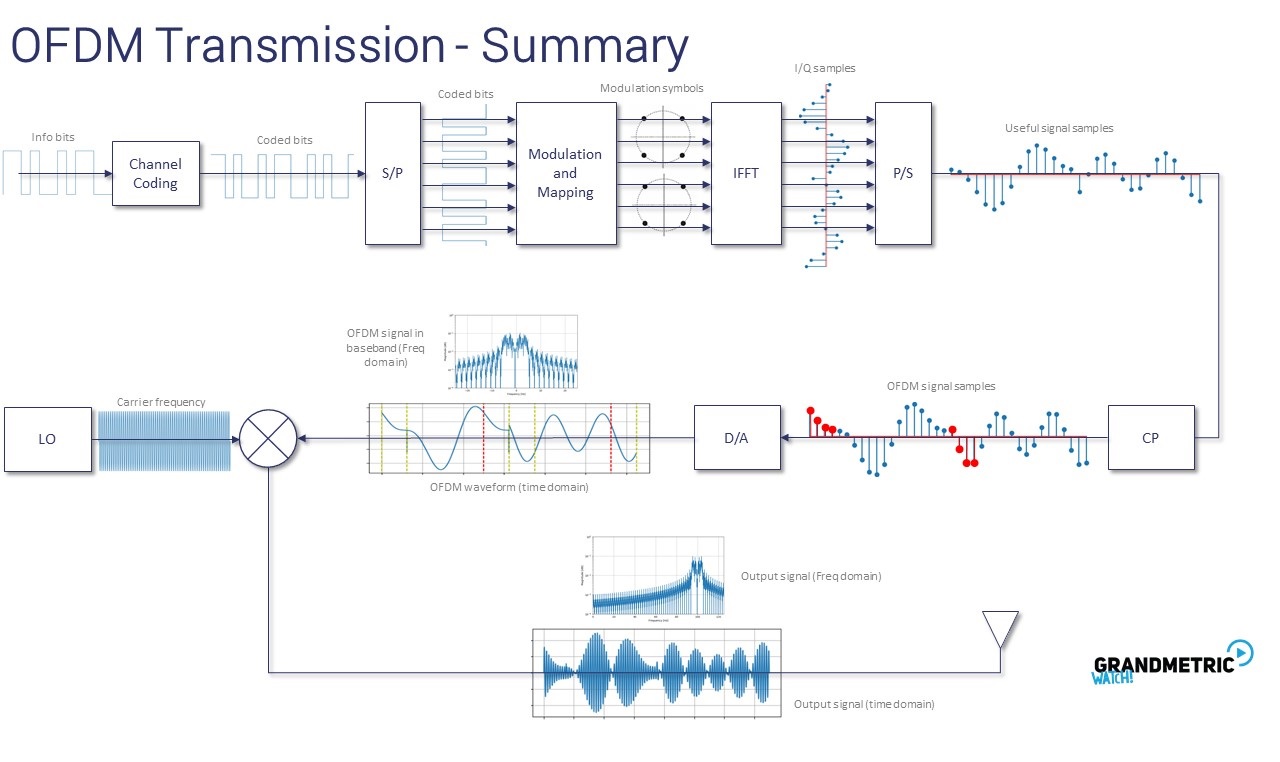
Stages of Data Transmission in LTE
- LTE eNB operates with IP packets. It receives IP packets and passes them to PDCP (Packet Data Convergence Protocol). PDCP layer supports header compression and it's performed according to RObust Header Compression (ROHC) defined by RFC 4995. An idea is to reduce size of upper layers headers (not only IP) as it contains static information. Especially it's important in case of VoIP packets transmission because of headers can represent more than a half of packet.
- After ROHC PDCP performs data encryption to secure user data and then adds PDCP header. PDCP header size is between 1 and 3 bytes.
- There is Radio Resource Scheduler that is a part of MAC (Media Access Control) layer. It collects all information about how many data are in buffers to be transmitted to each active UE, actual information about radio link quality to each UE, whether there are any packets to be retransmitted, each UE status (actually whether UE is listening to or is in power saving mode with turned off receiver for some time), schedule for system information transmissions (e.g. synchronization signals, Master Information Block, System Information Blocks). And based on all of this information scheduler each TTI (Transmission Time Interval, TTI = 1 ms) distributes radio resources among active UE and sets transmission parameters for each transmission. Also scheduler defines how many data can be transmitted within a TTI for a given UE and it's called as Transport Block Size (TBS) and set in bits.
- Once amount of data to be transmitted is known RLC (Radio Link Control) layer forms a packet (called as RLC PDU - RLC Packet Data Unit). This packet includes encrypted user data, PDCP header(s) and RLC header(s). Depending on allocation size for a given UE, RLC PDU can include a part of PDCP packet, a whole PDU packet or several PDU packets (as well as their parts). In case of packet segmentation and / or concatenation additional RLC subheader is added.
- After RLC, a packet goes to MAC layer where MAC header is added. Then the packet is divided into Transport Blocks based on TBS set by the scheduler. TBS depends on allocation size and MCS (Modulation and Coding Scheme). See more about Transport Block Size, MCS and LTE throughput calculation. Number of transport blocks is also defined by the scheduler and can be 1 or 2. Also CRC block is added to each transport block to distinguish between successful and unsuccessful data transmission on receiver side. CRC size is 24 bits.
- Then transport block is passed to Physical Layer where it's divided into Code Blocks. Each Code Block has its CRC (unless Transport Block size ≤ maximum Code Block size. In this case Transport Block CRC is used).
- Each Code Block is passed to Turbo encoder. Code rate is 1/3, i.e. there are three times more data on encoder output comparing to input. On output there are Systematic bits (represent 1/3 of encoder output) and Parity bits (represent 2/3 of encoder output). Output is stored into a ring buffer. There are as many ring buffers as a number of Code Blocks. In general the whole ring buffer can be transmitted or just a part of it. It depends on effective code rate (i.e. number of user bits to overall allocation size ratio) set by scheduler for a particular transmission. If data transmission is unsuccessful there will be retransmission scheduled and another part of ring buffer will be transmitted.
- Data from ring buffers are concatenated into Code Words. Number of code words equals to a number of Transport Blocks and can be 1 or 2. Code word size equals to Transport Block Size divided by effective code rate. Then it's modulated (see more about code rate and modulation), mapped to MIMO layers and radio resources, goes though IFFT (Inverse Fast Fourier Transform) and transmitted to radio module for over the air transmission.


















No comments:
Post a Comment
If You have any concern you are free to message/comment me.